Your The most widely used fourier series is images are ready in this website. The most widely used fourier series is are a topic that is being searched for and liked by netizens now. You can Find and Download the The most widely used fourier series is files here. Get all free photos and vectors.
If you’re looking for the most widely used fourier series is pictures information connected with to the the most widely used fourier series is interest, you have visit the right site. Our site always gives you suggestions for refferencing the maximum quality video and image content, please kindly surf and find more enlightening video articles and graphics that fit your interests.
The Most Widely Used Fourier Series Is. Fourier Series makes use of the orthogonality relationships of the sine and cosine functions. Let M be the unit circle. One of the most widely used applications is in calculating spectrograms. Here we think of the DFT or DCT as approximations for the Fourier series or cosine series of a function respectively in order to talk about its smoothness However the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries.
Fourier Series An Overview Sciencedirect Topics From sciencedirect.com
Cosθ 1 2 eiθ eiθ sinθ 1 2i eiθ eiθ Using these relations we can rewrite the ourierF series equation 1 in the more compact exponential notation. A similar problem arises for the DST in. What is the Fourier Series. An infinite series of the form in 8 called a Fourier series and the nipre sentation offunctions by Fourier series is one the most widely used techniques in applied mathematics especially for the solution of partial differential equations. Remains the most Widely used method of computing Fourier transforms 2. Let M be the unit circle.
In this section we consider applications of Fourier series to the solution of ODEs and the most well-known PDEs.
Remains the most Widely used method of computing Fourier transforms 2. Using the identity eiθ cosθisinθ We can write. In this section we consider applications of Fourier series to the solution of ODEs and the most well-known PDEs. The exponential Fourier series EFS is simpler and more compact. The original signal that changed over time is called the time domain representation of the signal. A most widely used special case of Fourier series is Fourier expansion.
Source: quora.com
In many applications you will nd that a more compact notation is used for the ourierF series. Now a lot of the systems that modify signals involve filters. Remains the most Widely used method of computing Fourier transforms 2. Using FFTs the process of computing DFTs and hence Fourier coefficients and Fourier series is now practically instantaneous. A Fourier series is a representation of a wave form or other periodic function as a sum of sines and cosines.
Source: lpsa.swarthmore.edu
Continuous Fourier transform spectroscopy refers to the scanning form of FTS in which by step moving one mirror the whole range of optical path difference is measured. A complete orthonormal basis of L 2 M is given as 12cosixsinixi 12. Let M be the unit circle. Let M be the unit circle. The heat equation u t k2u x2.
Source: lpsa.swarthmore.edu
A most widely used special case of Fourier series is Fourier expansion. Fourier Transform is a mathematical operation that breaks a signal in to its constituent frequencies. Therefore it is of no surprise that Fourier series are widely used for seeking solutions to various ordinary differential equations ODEs and partial differential equations PDEs. In their original paper Cooley and Tukey referred only to I. Remains the most Widely used method of computing Fourier transforms 2.
Source: sciencedirect.com
Cosθ 1 2 eiθ eiθ sinθ 1 2i eiθ eiθ Using these relations we can rewrite the ourierF series equation 1 in the more compact exponential notation. A Fourier series is a representation of a wave form or other periodic function as a sum of sines and cosines. Fourier Transform is a mathematical operation that breaks a signal in to its constituent frequencies. What is the Fourier Series. Although Fourier series is the basis of Fourier Transforms the most widely used component of the Fourier Analysis is the Fourier Transform.
Source: eeworldonline.com
Fourier series is a branch of Fourier analysis and it was introduced by Joseph Fourier. The original signal that changed over time is called the time domain representation of the signal. It is named after the French mathematician and physicist Jean-Baptiste Joseph Fourier 17681830. The Fourier transform is called the frequency domain representation of a signal since it depends on the frequency. What is the Fourier Series.
Source: youtube.com
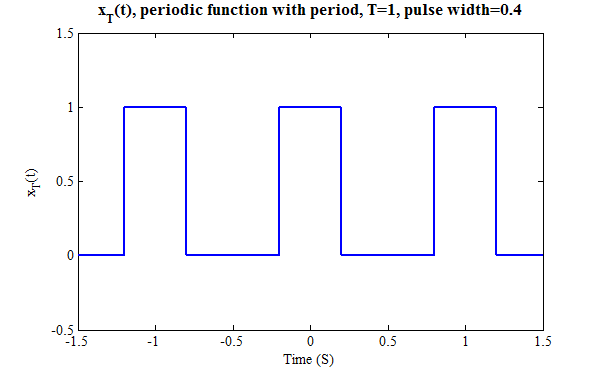
The heat equation u t k2u x2. 486 People Used More Courses View Course Fourier Series and. It serves as the basis for the Fourier integral the Laplace transform the solution of autonomous linear differential equations frequency response methods and. In this section we consider applications of Fourier series to the solution of ODEs and the most well-known PDEs. Any random segment of a signal is unlikely to have the same value at both the left and right boundaries.
Source: eeworldonline.com
Fourier Series makes use of the orthogonality relationships of the sine and cosine functions. In many applications you will nd that a more compact notation is used for the ourierF series. Here we think of the DFT or DCT as approximations for the Fourier series or cosine series of a function respectively in order to talk about its smoothness However the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries. This allows for rapid so-called real-time calculation of the frequency content of signals. In their original paper Cooley and Tukey referred only to I.
Source: researchgate.net
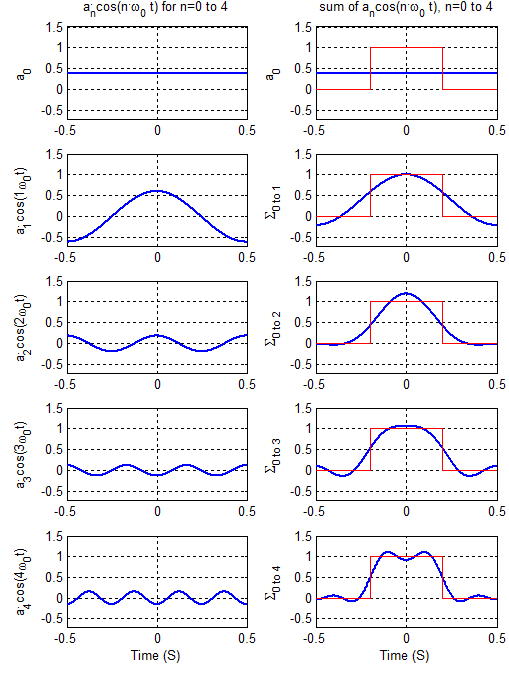
Since sound waves are made up of sine waves Fourier transforms are widely used in signal processing. Fourier series is a branch of Fourier analysis and it was introduced by Joseph Fourier. A Fourier series is an expansion of a periodic function fx in terms of an infinite sum of sines and cosines. An infinite series of the form in 8 called a Fourier series and the nipre sentation offunctions by Fourier series is one the most widely used techniques in applied mathematics especially for the solution of partial differential equations. Trigonometric Fourier series of xt is given as follows xta0n1ancosnω0tbnsinnω0t This can also be written in exponential form as below - xta0 an ejnw0tejnw0t 2 bn ejnw0tejnw0t 2j A n1 a0 anjbn 2.
Source: slideplayer.com
A Fourier series is a representation of a wave form or other periodic function as a sum of sines and cosines. Since sound waves are made up of sine waves Fourier transforms are widely used in signal processing. The Fourier transform is called the frequency domain representation of a signal since it depends on the frequency. Fx a 0 2 1 2 X n1 a i einx einx 1 2i X n1 b i. In this section we consider applications of Fourier series to the solution of ODEs and the most well-known PDEs.
Source: slideplayer.com
The Fourier series is the most widely used series expansion in mathematical modeling of engineering systems. And since filter design and implementation is a lot easier in frequency domain than it is in the time domain Fourier. One of the most widely used applications is in calculating spectrograms. Any random segment of a signal is unlikely to have the same value at both the left and right boundaries. Now a lot of the systems that modify signals involve filters.
Source: quora.com
Trigonometric Fourier series of xt is given as follows xta0n1ancosnω0tbnsinnω0t This can also be written in exponential form as below - xta0 an ejnw0tejnw0t 2 bn ejnw0tejnw0t 2j A n1 a0 anjbn 2. A similar problem arises for the DST in. Therefore it is of no surprise that Fourier series are widely used for seeking solutions to various ordinary differential equations ODEs and partial differential equations PDEs. Let M be the unit circle. Fx a 0 2 1 2 X n1 a i einx einx 1 2i X n1 b i.
Source: researchgate.net
Fourier series is a branch of Fourier analysis and it was introduced by Joseph Fourier. In their original paper Cooley and Tukey referred only to I. Hence this is most widely used. Any random segment of a signal is unlikely to have the same value at both the left and right boundaries. Therefore it is of no surprise that Fourier series are widely used for seeking solutions to various ordinary differential equations ODEs and partial differential equations PDEs.
Source: quora.com
Fourier series is a branch of Fourier analysis and it was introduced by Joseph Fourier. The Fourier series is the most widely used series expansion in mathematical modeling of engineering systems. Fourier Transform is a mathematical operation that breaks a signal in to its constituent frequencies. However It was soon discovered there are major differences between the Cooley-Tukey FFT and the algorithm described by Good. Fx a 0 2 1 2 X n1 a i einx einx 1 2i X n1 b i.
Source: sciencedirect.com
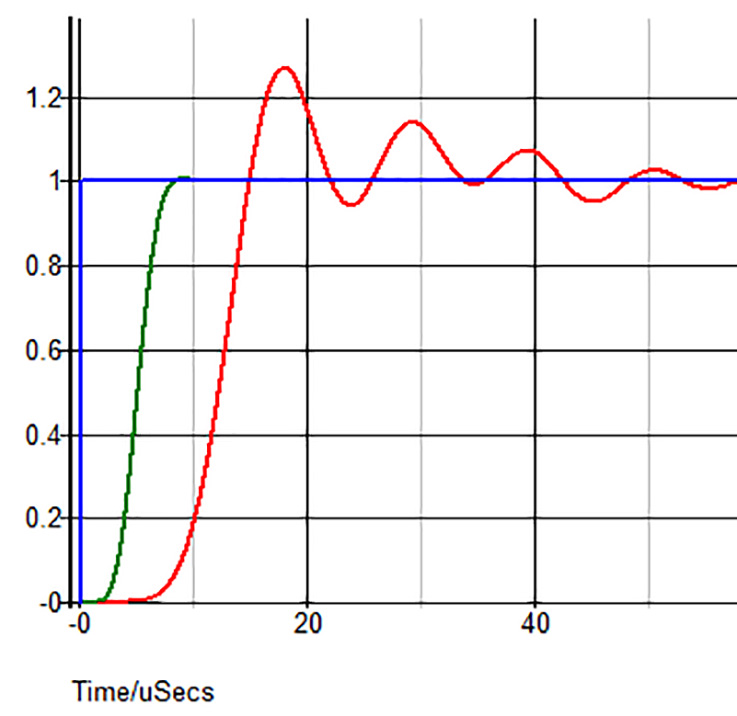
The Fourier transform is called the frequency domain representation of a signal since it depends on the frequency. This allows for rapid so-called real-time calculation of the frequency content of signals. Laurent Series yield Fourier Series. Here we think of the DFT or DCT as approximations for the Fourier series or cosine series of a function respectively in order to talk about its smoothness However the implicit periodicity of the DFT means that discontinuities usually occur at the boundaries. The Transform allows one to view the frequency domain representation of a signal.
Source: allsignalprocessing.com
It serves as the basis for the Fourier integral the Laplace transform the solution of autonomous linear differential equations frequency response methods and. Any random segment of a signal is unlikely to have the same value at both the left and right boundaries. Fx a 0 2 1 2 X n1 a i einx einx 1 2i X n1 b i. An infinite series of the form in 8 called a Fourier series and the nipre sentation offunctions by Fourier series is one the most widely used techniques in applied mathematics especially for the solution of partial differential equations. One of the most widely used applications is in calculating spectrograms.
Source: lpsa.swarthmore.edu
Therefore it is of no surprise that Fourier series are widely used for seeking solutions to various ordinary differential equations ODEs and partial differential equations PDEs. Let M be the unit circle. Using FFTs the process of computing DFTs and hence Fourier coefficients and Fourier series is now practically instantaneous. Since sound waves are made up of sine waves Fourier transforms are widely used in signal processing. It is named after the French mathematician and physicist Jean-Baptiste Joseph Fourier 17681830.
Source: quora.com
Continuous Fourier transform spectroscopy refers to the scanning form of FTS in which by step moving one mirror the whole range of optical path difference is measured. Laurent Series yield Fourier Series. The original signal that changed over time is called the time domain representation of the signal. In many applications you will nd that a more compact notation is used for the ourierF series. The Transform allows one to view the frequency domain representation of a signal.
Source: sciencedirect.com
Laurent Series yield Fourier Series. Fourier Transform is a mathematical operation that breaks a signal in to its constituent frequencies. Both the frequency domain representation of a signal and the process used. A complete orthonormal basis of L 2 M is given as 12cosixsinixi 12. Any random segment of a signal is unlikely to have the same value at both the left and right boundaries.
This site is an open community for users to do sharing their favorite wallpapers on the internet, all images or pictures in this website are for personal wallpaper use only, it is stricly prohibited to use this wallpaper for commercial purposes, if you are the author and find this image is shared without your permission, please kindly raise a DMCA report to Us.
If you find this site value, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title the most widely used fourier series is by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
